Transformasi Geometri: Pengertian, Jenis, Dan Rumus
templet indo
Transformasi Geometri: Pengertian, Jenis, dan Rumus
Transformasi Geometri: Pengertian, Jenis, dan Rumus
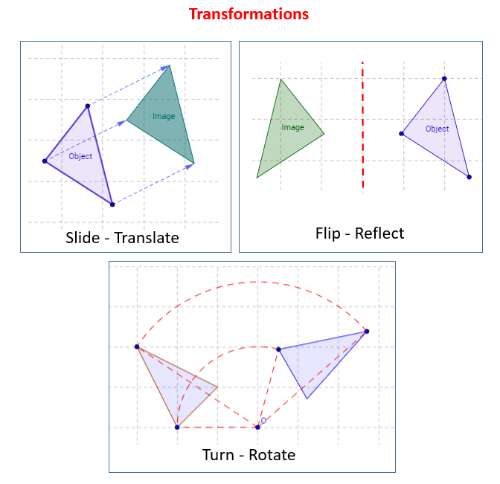
Transformasi Geometri: Pengertian, Jenis, dan Rumus
Transformasi geometri adalah perubahan bentuk, ukuran, atau posisi suatu objek geometri. Transformasi ini dapat dilakukan dengan berbagai cara, seperti translasi, rotasi, refleksi, dan dilatasi. Dalam artikel ini, kita akan membahas tentang pengertian, jenis, dan rumus transformasi geometri.
Pengertian Transformasi Geometri
Transformasi geometri adalah proses perubahan suatu objek geometri menjadi bentuk lain dengan mempertahankan beberapa sifat geometri aslinya. Transformasi ini dapat dilakukan dengan cara yang berbeda-beda, seperti menggeser, memutar, atau memantulkan objek.
Jenis Transformasi Geometri
Ada beberapa jenis transformasi geometri, yaitu:
- Translasi: Translasi adalah pergeseran objek geometri ke arah tertentu tanpa mengubah bentuk atau ukurannya.
- Rotasi: Rotasi adalah perputaran objek geometri sekitar suatu titik tertentu tanpa mengubah bentuk atau ukurannya.
- Refleksi: Refleksi adalah perlawanan objek geometri terhadap suatu garis atau bidang tertentu.
- Dilatasi: Dilatasi adalah perubahan ukuran objek geometri tanpa mengubah bentuknya.

Rumus Transformasi Geometri
Berikut adalah beberapa rumus transformasi geometri yang umum digunakan:
Translasi
Rumus translasi:
(x’, y’, z’) = (x + a, y + b, z + c)
di mana:
- (x, y, z) adalah koordinat titik asal
- (x’, y’, z’) adalah koordinat titik hasil translasi
- a, b, c adalah vektor translasi

Rotasi
Rumus rotasi:
(x’, y’, z’) = (x cos θ – y sin θ, x sin θ + y cos θ, z)
di mana:
- (x, y, z) adalah koordinat titik asal
- (x’, y’, z’) adalah koordinat titik hasil rotasi
- θ adalah sudut rotasi
Refleksi
Rumus refleksi:
(x’, y’, z’) = (2a – x, 2b – y, 2c – z)
di mana:
- (x, y, z) adalah koordinat titik asal
- (x’, y’, z’) adalah koordinat titik hasil refleksi
- (a, b, c) adalah koordinat titik refleksi
Dilatasi
Rumus dilatasi:
(x’, y’, z’) = (kx, ky, kz)
di mana:
- (x, y, z) adalah koordinat titik asal
- (x’, y’, z’) adalah koordinat titik hasil dilatasi
- k adalah faktor dilatasi
Kesimpulan
Transformasi geometri adalah perubahan bentuk, ukuran, atau posisi suatu objek geometri. Ada beberapa jenis transformasi geometri, seperti translasi, rotasi, refleksi, dan dilatasi. Rumus transformasi geometri dapat digunakan untuk menghitung koordinat titik hasil transformasi.
Contoh Soal
- Jika titik A memiliki koordinat (2, 3, 4) dan ditranslasikan sejauh 3 satuan ke arah x, maka koordinat titik A’ adalah?
Jawaban: (2 + 3, 3, 4) = (5, 3, 4)
- Jika titik B memiliki koordinat (4, 5, 6) dan dirotasikan sekitar sudut 90° terhadap sumbu z, maka koordinat titik B’ adalah?
Jawaban: (-5, 4, 6)
- Jika titik C memiliki koordinat (6, 7, 8) dan direfleksikan terhadap garis y = x, maka koordinat titik C’ adalah?
Jawaban: (7, 6, 8)
- Jika titik D memiliki koordinat (8, 9, 10) dan didilatasikan dengan faktor 2, maka koordinat titik D’ adalah?
Jawaban: (16, 18, 20)
Latihan Soal
- Jika titik E memiliki koordinat (3, 4, 5) dan ditranslasikan sejauh 2 satuan ke arah y, maka koordinat titik E’ adalah?
- Jika titik F memiliki koordinat (5, 6, 7) dan dirotasikan sekitar sudut 30° terhadap sumbu x, maka koordinat titik F’ adalah?
- Jika titik G memiliki koordinat (7, 8, 9) dan direfleksikan terhadap garis z = 0, maka koordinat titik G’ adalah?
- Jika titik H memiliki koordinat (9, 10, 11) dan didilatasikan dengan faktor 3, maka koordinat titik H’ adalah?
Jawaban
- (3, 4 + 2, 5) = (3, 6, 5)
- (5 cos 30° – 6 sin 30°, 5 sin 30° + 6 cos 30°, 7) = (3, 9, 7)
- (7, 8, -9)
- (27, 30, 33)
Kesimpulan
Transformasi geometri adalah perubahan bentuk, ukuran, atau posisi suatu objek geometri. Ada beberapa jenis transformasi geometri, seperti translasi, rotasi, refleksi, dan dilatasi. Rumus transformasi geometri dapat digunakan untuk menghitung koordinat titik hasil transformasi. Latihan soal dapat membantu memahami konsep transformasi geometri dengan lebih baik.
Penutup
Dengan demikian, kami berharap artikel ini telah memberikan informasi yang bermanfaat tentang Transformasi Geometri: Pengertian, Jenis, dan Rumus. Kami menghargai waktu Anda untuk membaca artikel ini. Nantikan artikel kami selanjutnya di artikel kami berikutnya!
