Rumus Turunan: Konsep Dan Aplikasinya
templet indo
Rumus Turunan: Konsep dan Aplikasinya
Rumus Turunan: Konsep dan Aplikasinya

Rumus Turunan: Konsep dan Aplikasinya
Turunan adalah salah satu konsep dasar dalam Analisis Matematika yang digunakan untuk menentukan laju perubahan suatu fungsi terhadap variabelnya. Dalam artikel ini, kita akan membahas tentang rumus turunan, jenis-jenis turunan, dan aplikasinya dalam berbagai bidang.
Apa itu Turunan?
Turunan suatu fungsi f(x) terhadap x adalah limit dari perbedaan fungsi terhadap x, yaitu:
f'(x) = lim(h → 0) [f(x + h) – f(x)]/h
Rumus di atas menunjukkan bahwa turunan suatu fungsi adalah limit dari perbedaan fungsi terhadap x, yang diukur dengan selisih nilai fungsi pada x dan x + h, dibagi dengan h.
Jenis-Jenis Turunan
Ada beberapa jenis turunan yang perlu kita ketahui:
- Turunan Pertama: Turunan pertama suatu fungsi f(x) adalah limit dari perbedaan fungsi terhadap x, yaitu f'(x).
- Turunan Kedua: Turunan kedua suatu fungsi f(x) adalah turunan dari turunan pertama, yaitu f”(x).
- Turunan Tingkat N: Turunan tingkat n suatu fungsi f(x) adalah turunan dari turunan tingkat n-1, yaitu f^(n)(x).
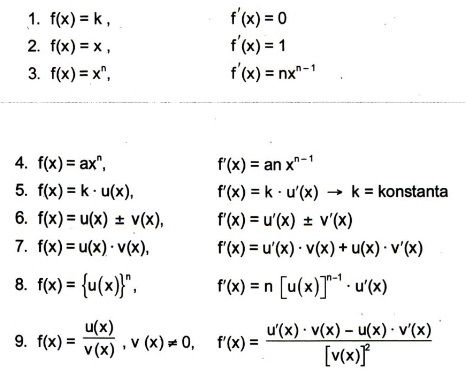
Rumus Turunan untuk Fungsi-Fungsi Sederhana
Berikut adalah beberapa rumus turunan untuk fungsi-fungsi sederhana:
- Turunan dari x^n: f'(x) = nx^(n-1)
- Turunan dari sin(x): f'(x) = cos(x)
- Turunan dari cos(x): f'(x) = -sin(x)
- Turunan dari e^x: f'(x) = e^x
- Turunan dari log(x): f'(x) = 1/x

Aturan-Aturan Turunan
Berikut adalah beberapa aturan turunan yang perlu kita ketahui:
- Aturan Turunan Konstanta: Turunan dari konstanta adalah nol.
- Aturan Turunan Penjumlahan: Turunan dari penjumlahan dua fungsi adalah penjumlahan turunan dari masing-masing fungsi.
- Aturan Turunan Perkalian: Turunan dari perkalian dua fungsi adalah perkalian turunan dari salah satu fungsi dengan fungsi lain.
- Aturan Turunan Pembagian: Turunan dari pembagian dua fungsi adalah pembagian turunan dari salah satu fungsi dengan fungsi lain.
Aplikasi Turunan dalam Fisika
Turunan memiliki aplikasi yang luas dalam fisika, terutama dalam mengukur laju perubahan posisi, kecepatan, dan percepatan objek. Berikut adalah beberapa contoh:
- Kecepatan: Kecepatan suatu objek dapat diukur dengan turunan dari posisi objek terhadap waktu.
- Percepatan: Percepatan suatu objek dapat diukur dengan turunan dari kecepatan objek terhadap waktu.
- Dinamika: Turunan dapat digunakan untuk menentukan gaya yang bekerja pada suatu objek berdasarkan percepatannya.
Aplikasi Turunan dalam Ekonomi
Turunan juga memiliki aplikasi dalam ekonomi, terutama dalam mengukur laju perubahan harga, produksi, dan konsumsi. Berikut adalah beberapa contoh:
- Elastisitas: Elastisitas harga suatu barang dapat diukur dengan turunan dari permintaan terhadap harga.
- Maksimalisasi: Turunan dapat digunakan untuk menentukan nilai maksimal dari suatu fungsi produksi atau konsumsi.
- Optimasi: Turunan dapat digunakan untuk menentukan nilai optimal dari suatu fungsi produksi atau konsumsi.
Kesimpulan
Turunan adalah konsep dasar dalam Analisis Matematika yang digunakan untuk menentukan laju perubahan suatu fungsi terhadap variabelnya. Rumus turunan dapat digunakan untuk menentukan laju perubahan posisi, kecepatan, dan percepatan objek dalam fisika, serta laju perubahan harga, produksi, dan konsumsi dalam ekonomi. Dengan memahami rumus turunan, kita dapat menyelesaikan berbagai masalah dalam berbagai bidang dengan lebih mudah dan akurat.
Penutup
Dengan demikian, kami berharap artikel ini telah memberikan pengetahuan yang berguna tentang Rumus Turunan: Konsep dan Aplikasinya. Kami berterima kasih atas perhatian Anda terhadap artikel kami. Sampai jumpa di artikel kami berikutnya!
