Rumus Luas Permukaan Kerucut: Konsep Dan Aplikasi
templet indo
Rumus Luas Permukaan Kerucut: Konsep dan Aplikasi
Rumus Luas Permukaan Kerucut: Konsep dan Aplikasi
Rumus Luas Permukaan Kerucut: Konsep dan Aplikasi
Kerucut adalah salah satu bentuk bangun ruang yang paling umum digunakan dalam berbagai bidang, seperti arsitektur, teknik sipil, dan matematika. Salah satu konsep penting dalam mempelajari kerucut adalah luas permukaannya. Pada artikel ini, kita akan membahas rumus luas permukaan kerucut, serta contoh-contoh aplikasinya dalam berbagai bidang.
Definisi Kerucut
Kerucut adalah bangun ruang yang memiliki alas berbentuk lingkaran dan dilingkupi oleh permukaan melengkung yang memancar dari pusat lingkaran. Kerucut dapat dibagi menjadi dua jenis, yaitu kerucut tegak dan kerucut miring.
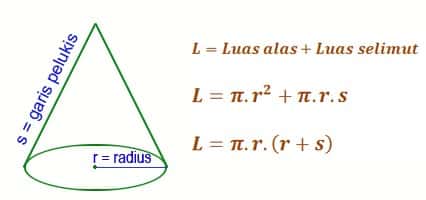
Rumus Luas Permukaan Kerucut
Luas permukaan kerucut (L) dapat dihitung menggunakan rumus berikut:
L = πr (√(r² + h²) + r)
di mana:
- L = luas permukaan kerucut
- π = konstanta pi (sekitar 3,14)
- r = jari-jari alas kerucut
- h = tinggi kerucut
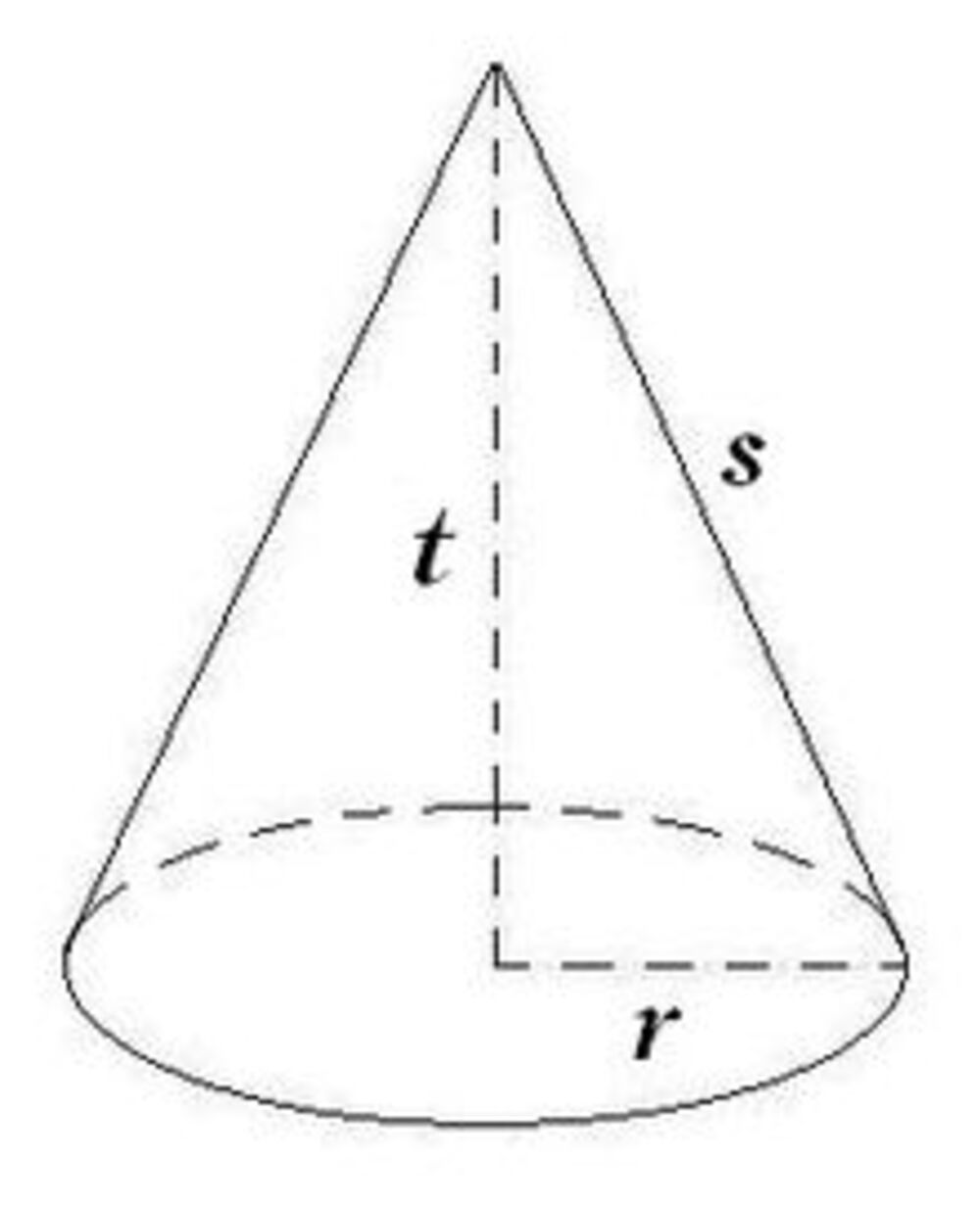
Rumus di atas dapat dibagi menjadi dua bagian, yaitu luas permukaan dasar (πr²) dan luas permukaan samping (πr√(r² + h²)).
Contoh Aplikasi
Berikut beberapa contoh aplikasi rumus luas permukaan kerucut dalam berbagai bidang:
- Arsitektur: Dalam merancang bangunan dengan atap kerucut, perlu dihitung luas permukaan atap untuk menentukan jumlah bahan yang dibutuhkan. Misalkan jari-jari alas atap adalah 5 meter dan tinggi atap adalah 10 meter. Luas permukaan atap dapat dihitung menggunakan rumus di atas.
L = π(5) (√(5² + 10²) + 5).jpg)
= 3,14(5) (√(25 + 100) + 5)
= 3,14(5) (√125 + 5)
= 3,14(5) (11,18 + 5)
= 3,14(5) (16,18)
= 251,44 m²
- Teknik Sipil: Dalam merancang jalan dengan kemiringan yang curam, perlu dihitung luas permukaan untuk menentukan jumlah bahan yang dibutuhkan. Misalkan jari-jari alas jalan adalah 10 meter dan tinggi jalan adalah 15 meter. Luas permukaan jalan dapat dihitung menggunakan rumus di atas.
L = π(10) (√(10² + 15²) + 10)
= 3,14(10) (√(100 + 225) + 10)
= 3,14(10) (√325 + 10)
= 3,14(10) (18,03 + 10)
= 3,14(10) (28,03)
= 879,32 m²
- Matematika: Rumus luas permukaan kerucut dapat digunakan untuk menghitung luas permukaan kerucut dalam contoh soal matematika. Misalkan jari-jari alas kerucut adalah 3 cm dan tinggi kerucut adalah 6 cm. Luas permukaan kerucut dapat dihitung menggunakan rumus di atas.
L = π(3) (√(3² + 6²) + 3)
= 3,14(3) (√(9 + 36) + 3)
= 3,14(3) (√45 + 3)
= 3,14(3) (6,71 + 3)
= 3,14(3) (9,71)
= 91,45 cm²
Kesimpulan
Rumus luas permukaan kerucut adalah konsep penting dalam mempelajari kerucut. Dengan menggunakan rumus ini, kita dapat menghitung luas permukaan kerucut dalam berbagai bidang, seperti arsitektur, teknik sipil, dan matematika. Contoh-contoh aplikasi di atas menunjukkan bagaimana rumus ini dapat digunakan dalam berbagai situasi. Oleh karena itu, perlu memahami rumus luas permukaan kerucut untuk dapat menerapkan konsep ini dalam berbagai bidang.
Penutup
Dengan demikian, kami berharap artikel ini telah memberikan pandangan yang baru tentang Rumus Luas Permukaan Kerucut: Konsep dan Aplikasi. Kami berharap Anda menemukan artikel ini informatif dan bermanfaat. Kami tunggu kehadiran Anda kembali di artikel kami berikutnya!
