Rumus Integral
templet indo
Rumus integral
Berikut adalah artikel tentang rumus integral dalam bahasa Indonesia sederhana.
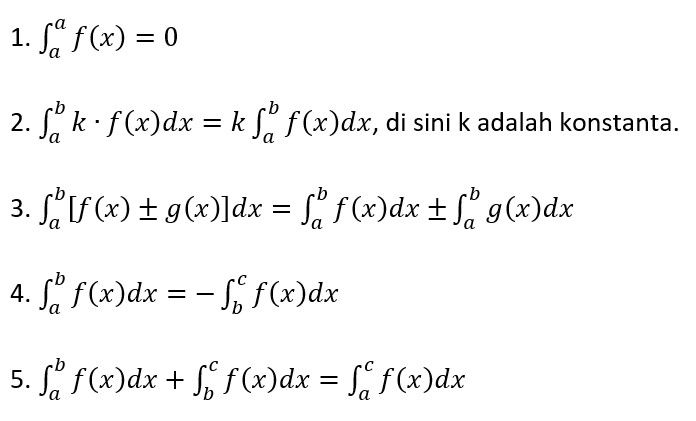
Berikut adalah artikel tentang rumus integral dalam bahasa Indonesia sederhana.
Pengertian Integral
Integral adalah suatu konsep dalam matematika yang digunakan untuk mencari luas daerah di bawah kurva fungsi. Integral juga dapat digunakan untuk mencari volume suatu benda yang memiliki bentuk tertentu. Dalam artikel ini, kita akan membahas tentang rumus integral yang sering digunakan dalam perhitungan matematika.
Jenis Integral
Terdapat dua jenis integral, yaitu:
- Integral Tak Tentu (Indefinite Integral): Integral tak tentu adalah integral yang tidak memiliki batas tertentu. Rumus integral tak tentu digunakan untuk mencari fungsi asli dari suatu fungsi.
- Integral Tentu (Definite Integral): Integral tentu adalah integral yang memiliki batas tertentu. Rumus integral tentu digunakan untuk mencari luas daerah di bawah kurva fungsi dalam interval tertentu.
Rumus Integral Tak Tentu

Berikut adalah beberapa rumus integral tak tentu yang sering digunakan:
- Integral Fungsi Polinom
∫x^n dx = (x^(n+1))/(n+1) + C
Contoh: ∫x^2 dx = (x^3)/3 + C
- Integral Fungsi Trigonometri
∫sin(x) dx = -cos(x) + C
∫cos(x) dx = sin(x) + C
∫tan(x) dx = -ln|cos(x)| + C
Contoh: ∫sin(x) dx = -cos(x) + C
- Integral Fungsi Eksponensial
∫e^x dx = e^x + C
Contoh: ∫e^x dx = e^x + C
Rumus Integral Tentu
Berikut adalah beberapa rumus integral tentu yang sering digunakan:
- Integral Fungsi Polinom
∫[a, b] x^n dx = [(b^(n+1))/(n+1)] – [(a^(n+1))/(n+1)]
Contoh: ∫[0, 2] x^2 dx = [(2^3)/3] – [(0^3)/3] = 8/3
- Integral Fungsi Trigonometri
∫[a, b] sin(x) dx = -cos(b) – (-cos(a))
∫[a, b] cos(x) dx = sin(b) – sin(a)
Contoh: ∫[0, π] sin(x) dx = -cos(π) – (-cos(0)) = 2
- Integral Fungsi Eksponensial
∫[a, b] e^x dx = e^b – e^a
Contoh: ∫[0, 2] e^x dx = e^2 – e^0 = e^2 – 1
Kesimpulan
Rumus integral adalah konsep yang sangat penting dalam matematika. Dalam artikel ini, kita telah membahas tentang rumus integral tak tentu dan integral tentu. Rumus integral tak tentu digunakan untuk mencari fungsi asli dari suatu fungsi, sedangkan rumus integral tentu digunakan untuk mencari luas daerah di bawah kurva fungsi dalam interval tertentu. Dengan memahami rumus integral, kita dapat mengerjakan soal-soal yang terkait dengan integral dengan lebih mudah.
Dalam perhitungan matematika, rumus integral sering digunakan dalam berbagai bidang, seperti fisika, teknik, dan ekonomi. Oleh karena itu, memahami rumus integral sangat penting bagi siswa dan praktisi matematika.
Contoh Soal Integral
Berikut adalah beberapa contoh soal integral:
- ∫x^2 dx = ?
- ∫[0, π] sin(x) dx = ?
- ∫[0, 2] e^x dx = ?
Jawaban:
- (x^3)/3 + C
- 2
- e^2 – 1
Tips Mengerjakan Soal Integral
Berikut adalah beberapa tips mengerjakan soal integral:
- Pahami rumus integral: Sebelum mengerjakan soal integral, pastikan Anda memahami rumus integral yang terkait.
- Identifikasi jenis integral: Pastikan Anda mengetahui apakah soal integral yang Anda hadapi adalah integral tak tentu atau integral tentu.
- Gunakan rumus integral yang tepat: Gunakan rumus integral yang tepat untuk mengerjakan soal integral.
- Kerjakan soal integral dengan hati-hati: Pastikan Anda mengerjakan soal integral dengan hati-hati dan tidak terburu-buru.
Dengan memahami rumus integral dan mengerjakan soal integral dengan hati-hati, Anda dapat meningkatkan kemampuan matematika Anda dan mengerjakan soal-soal yang terkait dengan integral dengan lebih mudah.
Penutup
Dengan demikian, kami berharap artikel ini telah memberikan informasi yang bermanfaat tentang Rumus integral. Kami menghargai waktu Anda untuk membaca artikel ini. Sampai jumpa di artikel kami berikutnya!

