Rumus Garis Singgung Lingkaran
templet indo
Rumus Garis Singgung Lingkaran
Rumus Garis Singgung Lingkaran
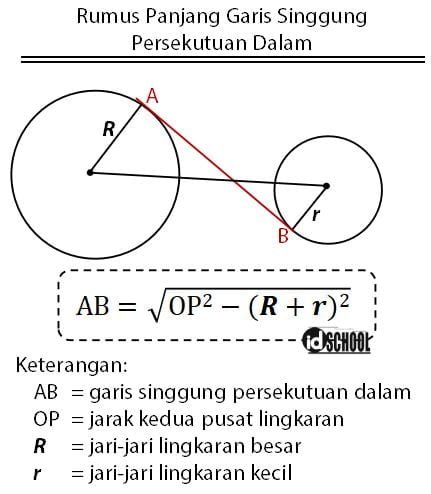
Rumus Garis Singgung Lingkaran
Lingkaran adalah bentuk dua dimensi yang memiliki ciri khas berupa titik pusat dan jari-jari. Garis singgung lingkaran adalah garis yang menyentuh lingkaran di sebuah titik dan tidak memotongnya. Dalam artikel ini, kita akan membahas tentang rumus garis singgung lingkaran dan cara menggunakannya.
Definisi Garis Singgung Lingkaran
Garis singgung lingkaran adalah garis yang memiliki gradien yang sama dengan gradien radius lingkaran di titik singgung. Artinya, jika kita tarik garis dari titik pusat lingkaran ke titik singgung, maka sudut antara garis singgung dan radius lingkaran adalah 90 derajat.
Rumus Garis Singgung Lingkaran
Rumus garis singgung lingkaran dapat dinyatakan dalam beberapa cara, yaitu:
- Rumus Garis Singgung dengan Titik Singgung
Rumus garis singgung lingkaran dengan titik singgung (x1, y1) adalah:
![]()
y – y1 = m(x – x1)
di mana:
- m adalah gradien garis singgung
- x1 dan y1 adalah koordinat titik singgung
- Rumus Garis Singgung dengan Jari-jari
Rumus garis singgung lingkaran dengan jari-jari r adalah:
y – y1 = m(x – x1)
(r)^2 = (x – x1)^2 + (y – y1)^2
di mana:
- m adalah gradien garis singgung
- x1 dan y1 adalah koordinat titik singgung
- r adalah jari-jari lingkaran
- Rumus Garis Singgung dengan Pusat
Rumus garis singgung lingkaran dengan pusat (h, k) adalah:
y – k = m(x – h)
(r)^2 = (x – h)^2 + (y – k)^2
di mana:
- m adalah gradien garis singgung
- h dan k adalah koordinat pusat lingkaran
- r adalah jari-jari lingkaran
Cara Menggunakan Rumus Garis Singgung Lingkaran
Berikut adalah contoh cara menggunakan rumus garis singgung lingkaran:
Contoh 1: Tentukan gradien garis singgung lingkaran dengan jari-jari 4 dan pusat (0, 0) di titik (3, 4).
Jawab: Gunakan rumus garis singgung lingkaran dengan jari-jari:
y – 4 = m(x – 3)
(4)^2 = (x – 3)^2 + (y – 4)^2
Karena titik singgung adalah (3, 4), maka kita dapat menyederhanakan persamaan menjadi:
4 = m(3 – 3)
0 = m(0)
Berdasarkan persamaan di atas, kita dapat menyimpulkan bahwa gradien garis singgung lingkaran adalah tidak terdefinisi (tidak dapat ditentukan).
Contoh 2: Tentukan persamaan garis singgung lingkaran dengan jari-jari 5 dan pusat (1, 2) di titik (6, 3).
Jawab: Gunakan rumus garis singgung lingkaran dengan pusat:
y – 2 = m(x – 1)
(5)^2 = (x – 1)^2 + (y – 2)^2
Karena titik singgung adalah (6, 3), maka kita dapat menyederhanakan persamaan menjadi:
3 – 2 = m(6 – 1)
1 = 5m
Berdasarkan persamaan di atas, kita dapat menyimpulkan bahwa gradien garis singgung lingkaran adalah 1/5. Selanjutnya, kita dapat menggunakan gradien ini untuk menentukan persamaan garis singgung lingkaran.
Kesimpulan
Rumus garis singgung lingkaran dapat digunakan untuk menentukan gradien dan persamaan garis singgung lingkaran. Dengan menggunakan rumus ini, kita dapat menyelesaikan berbagai masalah yang terkait dengan garis singgung lingkaran.
Referensi
- "Matematika", oleh Slamet Wirjosudirdjo
- "Geometri", oleh D. Djayasuputra
- "Lingkaran", oleh G. S. J. Meulenkamp
Pertanyaan dan Jawaban
Pertanyaan: Apa itu garis singgung lingkaran?
Jawab: Garis singgung lingkaran adalah garis yang menyentuh lingkaran di sebuah titik dan tidak memotongnya.
Pertanyaan: Bagaimana cara menentukan gradien garis singgung lingkaran?
Jawab: Gradien garis singgung lingkaran dapat ditentukan menggunakan rumus garis singgung lingkaran dengan titik singgung.
Pertanyaan: Apa itu rumus garis singgung lingkaran dengan jari-jari?
Jawab: Rumus garis singgung lingkaran dengan jari-jari adalah y – y1 = m(x – x1), di mana m adalah gradien garis singgung dan x1 dan y1 adalah koordinat titik singgung.
Penutup
Dengan demikian, kami berharap artikel ini telah memberikan pandangan yang baru tentang Rumus Garis Singgung Lingkaran. Kami berharap Anda menemukan artikel ini informatif dan bermanfaat. Sampai bertemu di artikel kami berikutnya!
